LOS NÚMEROS REALES

En matemáticas, los números reales (designados por ) incluyen tanto a los números racionales (positivos, negativos y el cero) como a los números irracionales; y en otro enfoque, trascendentes y algebraicos. Los irracionales y los trascendentes¹ (1970) no se pueden expresar mediante una fracción de dos enteros con denominador no nulo; tienen infinitas cifras decimales aperiódicas, tales como: , el número real log2, cuya trascendencia fue mentada por Euler en el siglo XVIII.²

Los números reales pueden ser descritos y construidos de varias formas, algunas simples aunque carentes del rigor necesario para los propósitos formales de matemáticas y otras más complejas pero con el rigor necesario para el trabajo matemático formal.

Durante los siglos XVI y XVII el cálculo avanzó mucho aunque carecía de una base rigurosa, puesto que en el momento no se consideraba necesario el formalismo de la actualidad, y se usaban expresiones como «pequeño», «límite», «se acerca» sin una definición precisa. Esto llevó a una serie de paradojas y problemas lógicos que hicieron evidente la necesidad de crear una base rigurosa para la matemática, la cual consistió de definiciones formales y rigurosas (aunque ciertamente técnicas) del concepto de número real.³En una sección posterior se describirán dos de las definiciones precisas más usuales actualmente: clases de equivalencia desucesiones de Cauchy de números racionales y cortaduras de Dedekind.

Los números reales son los números que se puede escribir con anotación decimal, incluyendo aquellos que necesitan una expansión decimal infinita. El conjunto de los números reales contiene todos los números enteros, positivos y negativos; todos los fracciones; y todos los números irracionales -- aquellos cuyos desarrollos en decimales nunca se repiten. Ejemplos de números irracionales son
√2 = 1.4142135623730951 . . .     π = 3.141592653589793 . . .     e = 2.718281828459045 . . .

Es muy útil representar a los números reales como puntos en la recta real, como mostrado aquí.

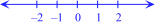
Observe que los números más mayores aparecen a la derecha: Si a < b entonces el punto corresponde a b estrá a la derecha del punto que corresponde a a.

Ejemplo:

2+8 = 8+2 5(-3) = ( -3)5

Propiedad: Asociativa

Operación: Suma y Multiplicación

Definición: a+(b+c)=(a+b)+c------ a(bc) = (ab)c

Que dice:
Puedes hacer diferentes asociaciones al sumar o multiplicar reales y no se afecta el resultado.

Ejemplo:

7+(6+1)=(7+6)+1 -2(4x7)= (-2x4)7

Propiedad: Identidad

Operación: Suma y Multiplicación

Definición: a + 0 = a------ a x 1= a
Que dice: Todo real sumado a 0 se queda igual; el 0 es la identidad aditiva. Todo real multiplicado por 1 se queda igual; el 1 es la identidad multiplicativa.

Ejemplo:

-11 + 0 = -11 17 x 1 = 17

Propiedad: Inversos

Operación: Suma y Multiplicación

Definición: a + ( -a) = 0------(a)1/a=1

Que dice:
La suma de opuestos es cero. El producto de recíprocos es 1.

Ejemplos:

15+ (-15) = 0 1/4(4)=1

Propiedad: Distributiva

Operación: Suma respecto a Multiplicación

Definición: a(b+c) = ab + ac

Que dice:
El factor se distribuye a cada sumando.

Ejemplos:

2(x+8) = 2(x) + 2(8)

Propiedades de las igualdades

Propiedad Reflexiva

Establece que toda cantidad o exprecion es igual a si misma.

Ejemplo:

2a = 2a; 7 + 8 = 7 + 8; x = x

Propiedad Simétrica

Consiste en poder cambiar el orden de los miembros sin que la igualdad se altere.

Ejemplo:

Si 39 + 11 = 50, entonces 50 = 39 + 11
Si a - b = c, entonces c = a - b
Si x = y, entonces y = x

Propiedad Transitiva
Enuncia que si dos igualdades tienen un miembro en común los otros dos miembros también son iguales.
Ejemplo:
Si 4 + 6 = 10 y 5 + 5 = 10, entonces 4 + 6 = 5 + 5...