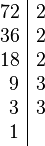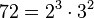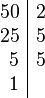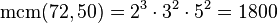¿Que es el algebra?
El álgebra es una rama de las matemáticas que se ocupa de estudiar las propiedades generales de las operaciones aritméticas y lo números para generar procedimientos que puedan globalizarse para todos los casos análogos esta rama se caracteriza por hacer implícitas las incógnitas dentro de la misma operación; ecuación algebraica.
Etimologicamente, proviene del árabe (también nombrado por los árabes Amucabala )??? (yebr) ( al-dejaber), con el significado de reducción, operación de cirugía por la cual se reducen los huesos luxados o fraccionados (algebrista era el médico reparador de huesos).
Historia del álgebra
El álgebra tuvo sus primeros avances en las civilizaciones de Babilonia y Egipto, entre el cuarto y tercer milenio antes de Cristo. Estas civilizaciones usaban primordial mente el álgebra para resolver ecuaciones de primer y segundo grado.
El álgebra continuó su constante progreso en la antigua Grecia. Los griegos usaban el álgebra para expresar ecuaciones y teoremas, un ejemplo es el teorema de pitagoras. Los matemáticos más destacados en este tiempo fueron Arquimesas Herón y Diofante. Arquímedes se basó en las matemáticas en su tratados de física y geometría del espacio. Herón fue otro que se basó en ellas para hacer algunos de sus inventos, como la primera máquina de vapor. Diofante fue el griego que más contribuyó a esta área del conocimiento, como principales trabajos tenemos al análisis diofántica y la obra de Las Aritméticas, que recopila todo el conocimiento del álgebra hasta ese entonces.
Como consecuencia, el álgebra cambió de rumbo y amplió su dominio a todas las teorías que se habían inventado alrededor del tema inicial, incorporando las teorías de los grupos matemáticos y sus extensiones,y parte de la geometría la rama relacionada con los polinomios de segundo grado de dos variables, es decir las cónicas elipse, parábola, hipérbola círculo, ahora incluidas en el álgebra bilineal.
El álgebra se fundió con éxito con otras ramas de las matemáticas como la lógica ( álgebra de Boole), el análisis y la topología.¿Que es la Aritmetica?
La Aritmetica es una rama de las matematicas que se encarga de estudiar las estrucutras númericas elementales, asi como las propiedades de las operaciones y los números en si mismos en su concepto mas profundo, construyendo lo que se conoce como teoria de números.
Para ti es mas sencillo encontrar la aritmetica dentro de tu vida cuando:
- vas a la tienda a comprar algo, y te ves en la necesidad de calcular por medio de una resta, el cambio que dara el tendero.
- cuando estas a punto de a abordar el servicio publico y cuantas rapidamente la cantidad de dinero necesaria para pagar el valor del pasaje.
- tambien cuando haces la cuenta o inventario de tus cosas.



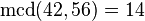

 entonces
entonces 
 es un entero,
es un entero, 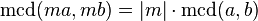
 es un número primo, entonces
es un número primo, entonces  o bien
o bien 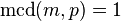
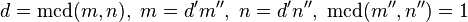 , entonces
, entonces 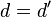
 es un divisor común de
es un divisor común de  , entonces
, entonces 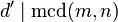
 , entonces
, entonces