Un número decimal, por definición, es la expresión de un número no entero, que tiene una parte decimal. Es decir, que cada número decimal tiene una parte entera y una parte decimal que va separada por una coma, y son una manera particular de escribir las fracciones como resultado de un cociente inexacto.
La parte decimal de los valores decimales se ubica al lado derecho de la coma y en la recta numérica, esta parte estaría ubicada entre el cero y el uno, mientras que la parte entera se la escribe en la parte derecha. En el caso de que un número decimal no posea una parte entera, se procede a escribir un cero al lado izquierdo o delante de la coma. Aquí varios ejemplos para ilustrar estos casos:
7,653
En este valor podemos ver que el número entero se encuentra primero es siete o 7, delante de la coma o a su izquierda, mientras que la parte decimal, que en es te caso contra de tres cifras es 653 y se encuentra a la derecha de la cifra.
0,23
En este otro ejemplo, vemos que la parte decimal tiene solo dos cifras, pero la parte entera se reduce a cero, por lo tanto se deduce que la parte entera es nula y debe ser expresada de esa manera.
4 + 0,23 = 4,23
Este ejercicio nos demuestra como la parte entera se une con la parte decimal a través de una suma que indica que la parte entera es 4 mientras que la parte decimal se reduce a un número menor que uno pero mayor que cero, en este caso 0,23.
Clasificación de los números decimales
Existen varias formas de separar los números decimales; puede ser con una coma, con un punto o con un apóstrofe según se acostumbre y se desee, pero también existen varias formas de números decimales, entre los que tenemos:
Números decimales exactos.- estos son valores cuya parte decimal posee un número limitado de cifras decimales y se pueden escribir sin un excesivo esfuerzo, como estos:
0,75; 2,6563; 6,32889
Números decimales periódicos.- son aquellos que tienen un número ilimitado o infinito de cifras decimales, pero que se repiten en un patrón o período determinado que es visible dentro de un número de cifras variable en cada caso. Para denotar que se trata de un número infinito, que no puede ser escrito indefinidamente por un ser humano, se utilizan tres puntos seguidos que significa infinidad, por ejemplo.
1,333333333…; 6,0505050505…; 5,325483254832548…
Números decimales periódicos puros.-donde los números decimales son parte del mismo grupo como:
3,63636363…
Números decimales periódicos mixtos.- donde existen cifras que están fuera del periodo o patrón de cifras decimales, como en:
9,36666666…
Números decimales no periódicos.- estos números tienen cifras decimales infinitas que no pueden ser definidas como un patrón, un buen ejemplo de números decimales no periódicos, son los números irracionales, como:
El número Pi, o como se lo conoce mejor con su símbolo π. Su valor es el cociente entre la longitud o perímetro de la circunferencia y la longitud de su diámetro. De él se han calculado millones de cifras decimales y aún sigue sin ofrecer un patrón. La aproximación de su número es 3.141592653589…
Composición de un número decimal
Los números decimales se componen de cifras que son separadas de la parte entera con una como, un punto o un apóstrofe, como se señalaba en la parte anterior. Pero estas cifras también tienen una característica que las diferencia según la posición de su denominador. Las décimas se ubican un lugar después de la coma o separador; las centésimas están dos lugares después del separador; las milésimas en el tercer lugar y así podríamos seguir con las diezmilésimas, las cienmilésimas, etc.
Por ejemplo en el número 7,951 notamos que 7 es la parte entera, 9 es la décima, 5 es la centésima y 1 es la milésima.
Operaciones con números decimales
Suma y resta
Para sumar y restar números decimales, debemos anotar cada valor en forma vertical, para facilitar la operación, de tal manera que la coma quede en la misma columna, incluso si la parte entera de un valor tenga más cifras que el otro, como se ve en el ejemplo siguiente:
3,48
9,657
A continuación, se iguala el número de cifras decimales de cada valor si es necesario, añadiendo uno o varios ceros al valor con menos cifras decimales para que queden con el mismo número, pues el cero añadido a la derecha de la parte decimal no altera el valor, así:
3,480
9,6570
Finalmente se suma de manera tradicional, sin tomar en cuenta la coma, y al resultado final se le añade la coma en l misma posición que se encuentra en ambos valores sumados o restados.
3,480
+9,657
=13,137
Multiplicación
Para multiplicar dos números decimales, o un número decimal por un número entero, se resuelve la operación sin tomar en cuenta la coma. Luego el número de cifras decimales será la suma del número de cifras decimales de los dos factores, es decir que si un factor tiene dos cifras decimales y el otro tiene una cifra decimal, quiere decir que el resultado deberá tener tres cifras decimales, como en el siguiente ejemplo
3,25 x 2,7
325
X27
2275
650
=8,775
Ahora con un ejemplo, como multiplicar un número decimal por un entero, donde simplemente se siguen las reglas anteriores, con la diferencia de que el número entero tiene cero cifras decimales por lo tanto el número de cifras decimales del resultado se mantiene como en el factor decimal, veamos:
3,25 x 2
325×2=650
=6,50
Para multiplicar números decimales por cifras que son múltiplos de diez, solo recorremos la coma hacia la derecha tantos espacios como ceros tenga el múltiplo de diez, y en el caso de que tengamos que seguir recorriendo y ya no haya cifras decimales, añadimos ceros al resultado, de esta manera:
3,568×10 = 35,68
3,568×100 = 356,8
3,568×1000 = 3568
3,568×10000 = 35680
División
Para dividir números decimales, tenemos varios casos según los decimales se encuentren en el divisor, en el dividendo o en ambos.
Para dividir cuando el dividendo es decimal, se hace la división sin tomar en cuenta la coma y al obtener la primera cifra decimal, se pone la coma en el resultado y se sigue dividiendo de la misma manera.
526,6562 / 7
36 75,2366
16
25
46
42
0
Para dividir cuando el decimal se encuentra en el divisor, se debe recorrer la coma hasta el final de la cifra del divisor, mientras que en el dividendo se añaden ceros por el mismo número de espacios recorridos por la coma. Y se procede a dividir de manera normal.
6824 / 36,58
682400 / 3658
Cuando el dividendo y el divisor son números decimales, recorremos las comas por tantos espacios sean necesarios para que desaparezca del número con más cifras decimales. Mientras que en el número que tiene menos cifras decimales se irán añadiendo ceros según los espacios que falten, y se procede a dividir de la manera tradicional.
32,698 / 8,25
32698 / 8250
Para dividir un número decimal para una cifra múltiplo de diez se debe retroceder la coma hacia la izquierda según el número de ceros que tenga el múltiplo de diez, y si excede el número de espacios, se debe añadir ceros mientras se mantiene la coma y un cero a su izquierda, como a continuación.
3568/10 = 356,8
3568/100 = 35,68
3568/1000 = 3,568
3568/10000 = 0,3568
3568/100000 = 0,03568



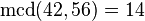

 entonces
entonces 
 es un entero,
es un entero, 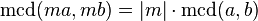
 es un número primo, entonces
es un número primo, entonces  o bien
o bien 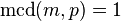
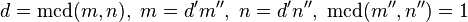 , entonces
, entonces 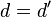
 es un divisor común de
es un divisor común de  , entonces
, entonces 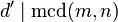
 , entonces
, entonces 

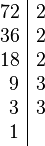
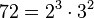
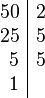

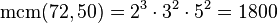

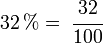


 . Ejemplos:
. Ejemplos:  , etc.
, etc. generan la
generan la 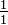 ).
).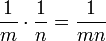




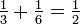



 .
.